Bar-and-joint rigidity in the plane
Bar-and-joint rigidity in the plane
Planar bar-and-joint frameworks:
A planar bar-and-joint framework is a structure made of fixed-length bars connected by universal joints, with full rotational freedom. The allowed motions are those that preserve the lengths and connectivity of the bars. (The bars are allowed to "pass through" each other.) When the only allowed motions are those that preserve the distance between every pair of joints, the framework is said to be rigid. Otherwise it is flexible.
A framework with three bars making a triangle must be rigid, since all the possible distances are fixed by bars. A rigid framework in the plane has three trivial degrees of freedom: one rotational and two translational.
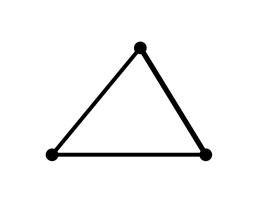
Rigid
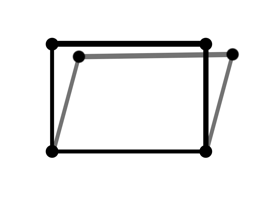
Flexible
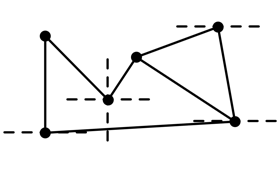
On the other hand, a four-bar mechanism has a non-trivial motion, which implies that it is flexible. Since this motion is allowed even when an edge of the framework is pinned down to factor out trivial degrees of freedom, this motion is called an internal motion.
Laman's theorem and combinatorial rigidity:
The most fundamental question we can ask about a framework is whether it is rigid or flexible. For almost all planar bar-and-joint frameworks, Laman's foundational theorem gives a combinatorial answer. We associate each framework with a graph that has one vertex for each joint and one edge for each bar. (Notice that many different frameworks can have the same graph.)
Theorem (Laman):
Let G be a graph with n vertices and m edges. G is the graph of a generic minimally rigid framework if and only if: any subset of n' vertices in G spans at most 2n'-3 edge; and m=2n-3.
The genericity condition in Laman's theorem holds for almost all choices for the lengths of the bars for a given graph G. Genericity is a somewhat technical concept, but it can be intuitively thought of as playing the role of "general position" assumptions that are a paradigmatic part of computational geometry.
Rigid components and redundant edges:
Laman's theorem gives a combinatorial method for analyzing the rigidity of frameworks by counting the number of bars. For example, we can see that the triangle is minimally rigid, since 3=2×3-3 and all the subgraphs satisfy the Laman count. The four-bar mechanism must be flexible, since it 4<2×4-3=5.
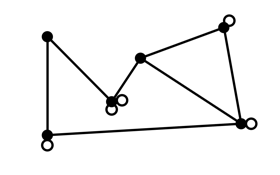
Flexible frameworks still may contain substructures that move rigidly. We call a set of vertices a rigid component if it is inclusionwise maximal with the property all of the vertices in the set move rigidly with respect to each other. Since the endpoints of every bar move rigidly with respect to each other, we see that every joint much be in some rigid component. In the example of the four-bar mechanism, each bar forms one rigid component.

Rigid components

Rigid components and redundant edges
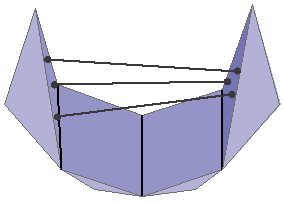
Rigid components of flexible frameworks need not be (and in general, will not be) single edges. In the examples above, both frameworks have one internal motion, similar to that the four-bar mechanism. However, both have a larger rigid component, highlighted in red. The example on the left, like the four-bar mechanism, does not have enough edges to be rigid.
On the right is a framework that does have enough bars to be, but it violates the Laman counts on the set of vertices shown in red. This means that there is some edge that can be removed from the framework without changing its rigidity properties. We call such an edge redundant, and such a set of vertices over constrained. Observe that there is not a single edge that is redundant in this case: removing any of the edges spanned by the highlighted set of vertices results in a framework with the same rigid components as the original. We also see here that rigid components need not be minimally rigid substructures of a framework.