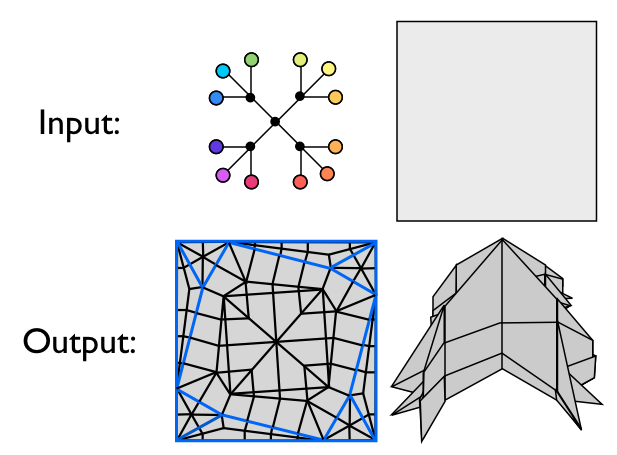
The origami design problem solved by TreeMaker.
A full description of the algorithm is beyond the scope of this website. On his website Lang provides a nice overview of his theory of uniaxial bases, the freely downloadable TreeMaker software, lots of good documentation, and a plethora of beautiful origami sculptures that Lang has made using the software. We include here only the details necessary to motivate our later discussion of univeral molecules.
Lang's TreeMaker algorithm solves the following version of the origami design problem: Given a desired shadow tree and polygonal sheet of paper, Lang's version of the problem is to produce a crease pattern for the paper such that there exists a uniaxial base whose shadow tree is the input tree.

The origami design problem solved by TreeMaker.
TreeMaker does this by first spreading vertices across the face of the paper which represent the leaves of the tree subject to the constraints that the distance on the paper between two vertices must be greater than or equal to the corresponding distance in the tree (up to a constant scaling factor).
Edges are then added between vertices where this distance is equal subdividing the paper into a set of polygons each with an associated subtree. Each convex polygon, if convex, is then independently filled in with a crease pattern via Lang's Universal Molecule algorithm. Finally, the crease pattern for the paper is formed by gluing together the crease patterns for each polygon. This is illustrated below.
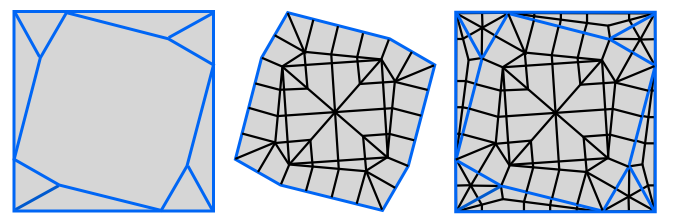
The paper is subdivided into convex polygons each of which is independently filled with a crease pattern by Lang's Universal Molecule algorithm.