Lang's Universal Molecule Algorithm

The input to Lang's Universal Molecule Algorithm is a topologically embedded metric tree and a special kind of convex polygon we call a Lang Polygon. The output is a crease pattern for which there exists a folded realization as a uniaxial base whose shadow tree is the input metric tree. The figure below illustrates the input and output for the algorithm.

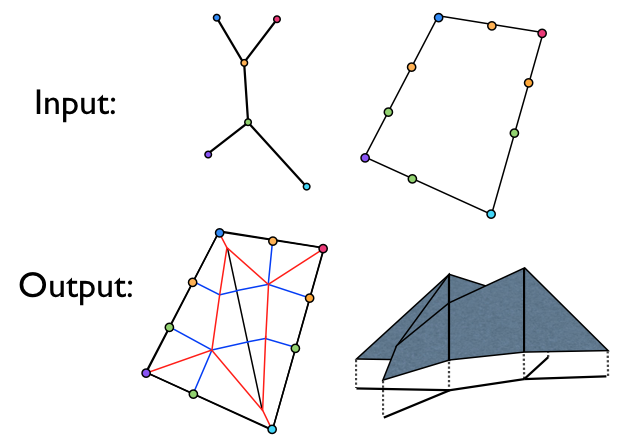
The input/output of Lang's Universal Molecule Algorithm.

The algorithm works by a parallel sweep process in which the edges of the Lang polygon are moved inwards in a parallel fashion at constant speed. The interior sweeping polygon is called a contour. The distance the edges have moved at any point in the sweep process is called the height of the contour.

The parallel sweep process.

Edges of the crease pattern are created by tracing the paths of the vertices of the polygon (see figure below).

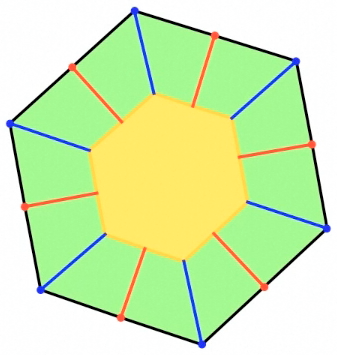
The crease pattern edges (red and blue) are created by tracing the vertices of the Lang polygon during the sweep.

As the contour sweeps inwards, an edge between two marker vertices maintains its length, while an edge between a marker and a corner shrinks. This corresponds to a shrinking of the tree by moving the leaves inwards. In the figure below, the pink tree (right) superimposed on the input tree corresponds to the contour (left) in the sweeping process. The distances between markers for b1 adn b2 along the contour do not change during the sweep, which is reflected in the shrinking tree.

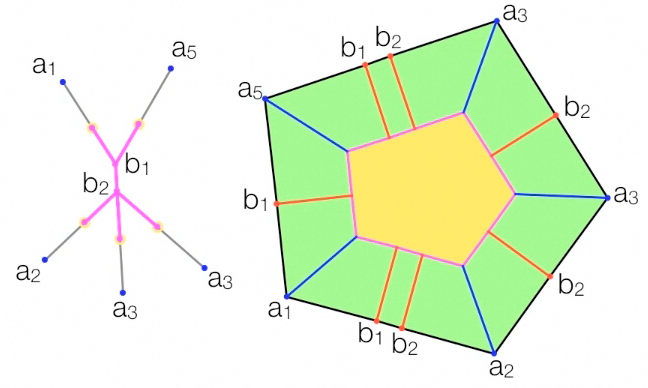
The crease pattern edges (red and blue) are created by tracing the vertices of the Lang polygon during the sweep.

At certain discrete heights, one of two events occurs. A contraction event occurs when an edge between a corner and a marker vertex shrinks to a single point. Note that all leaves incident to the same node, shrink at once.

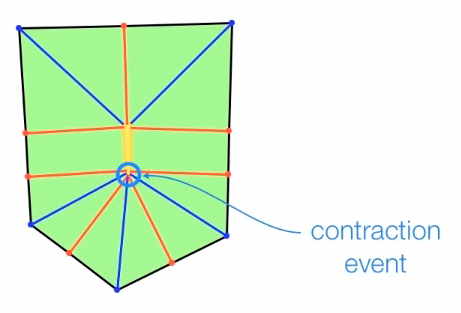
A contraction event.

In a splitting event, the distance between two corner vertices is equal to the distance between the corresponding leaf nodes. At this point, if the sweeping process proceeds, the contour would cease to be a Lang polygon. In the illustration below, the distance between leaves a1 and a2 in the shrunken tree is equal to the distance between vertices a1 and a2 in the contour.

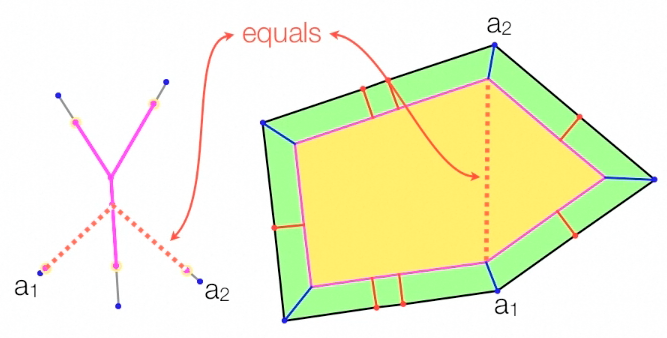
A branching event.

The contour is therefore split by adding an edge between the two corner nodes. Marker nodes are added along this new edge so that the edge corresponds to the path in the tree between the two leaf nodes.

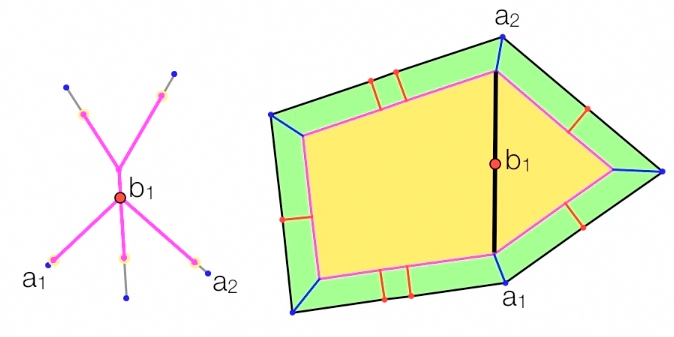
Splitting the contour at a branching event.

In the tree, this split corresponds to a splitting of the tree into two trees along the path between the two leaf nodes.

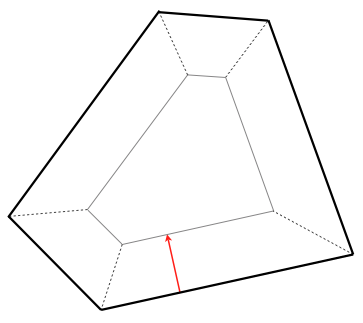
In 3D the sweeping contours correspond to a sweeping process of the shrinking tree upwards by the height of the contour.

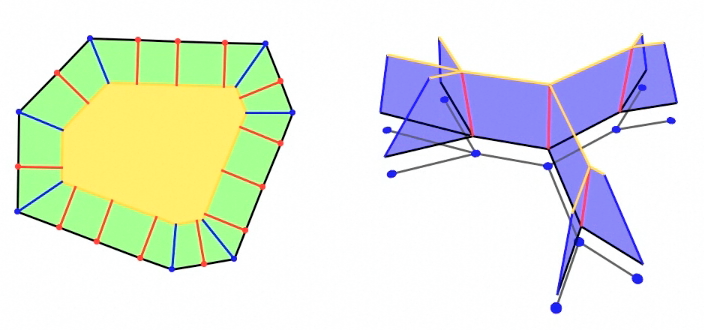
The sweep in 3D.

Conceptually, the sweeping process is a continuous process with discrete events. The algorithm, however, works by identifying the height of the next event, and by recursing on the contour and sub-tree at that event. The base case is when the next event is a contraction of all edges to the same vertex. In the illustration below the gray lines represent the actual discrete event contours on which the algorithm is invoked. The intermediate sweep lines are generated for illustration purposes only.

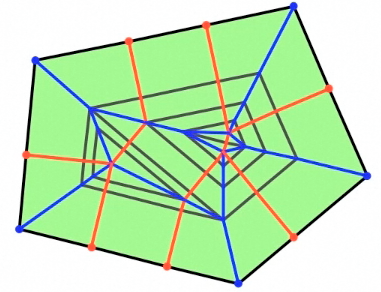
The gray lines indicate the actual contours that the algorithm recurses on.

Using the demo:

The demo has a split pane with two editors. The tree editor on the left allows you to edit the tree by adding nodes and arcs. You can change edit modes from nodes to arcs by clicking on the "Nodes" or "Arcs" button. Once you have a tree defined, the "flaps" edit mode allows you to rotate leaf nodes around their parents while maintaining arc length. The "››" button generates a doubling cycle for the tree in the polygon editor on the right.

The polygon editor on the right allows you to drag the corner points of the doubling cycle to turn it into a Lang polygon. Red dotted lines between corner vertices represent vertices whose distance is less than their corresponding distance in the tree, thus violating the definition of a Lang polygon. Once all of these constraints are removed, you will see only the green polygon.

Note: In the current version it is possible to invert the ordering of the polygon nodes such that the walk of the tree corresponds to a clockwise, rather than counter-clockwise walk of the polygon. In this case the vertex labels will fall inside the polygon rather than outside it and the output is undefined, since our implementation assumes that the walk of the inner face is counter-clockwise. Future updates will address this limitation.

Once you have a polygon defined, drag the sweep slider above the the polygon editor to view the sweeping process as it generates the crease pattern. You can continue to edit the vertices of the polygon and see the crease pattern update live. If, however, you modify the tree, you will need to click on the "››" button to generate a new doubling cycle for the tree.

This version does not show the 3D uniaxial base for the crease pattern. We also have a live demo which visualizes the 3D base as well. This demo requires that Java's implementation of OpenGL be allowed to run on your computer and thus requires that you grant the applet special permissions when it is run. If you want to run that version, please click here, and accept whatever Java dialogs are presented.

In the polygon edit window (left), the scroll wheel (or two finger scroll on a Mac laptop) can be used to zoom in and out.

Note: This applet requires Java 1.6 to run. Also, we have experienced problems running the applet in Safari 5.1.2 (Safari 5.1.3 appears to work fine). If you experience any problems running the applet, please try a different browser (e.g. Google Chrome or Firefox). If this does not work, please send an email jbowers "at" cs "dot" umass "dot" edu.